POLA BILANGAN

Pola bilangan sendiri memiliki arti suatu susunan bilangan yang memiliki bentuk teratur atau suatu bilangan yang tersusun dari beberapa bilangan lain yang membentuk suatu pola . Dan pola bilanga juga memiliki banyak jenisnya atau macamnya .

Macam – macam Pola Bilangan

Macam – macam pola bilngan meliputi beberapa jenis berikut ini :

1.      Pola Bilangan Ganjil 

Poal bilangan ganjil yaitu pola bilangan yang terbentuk dari bilangan – bilangan ganjil. Sedangkan pengertian dari bilangan ganjil sendiri memiliki arti suatu bilangan asli yang tidak habis dibagi dua ataupun kelipatannya.

a.       Pola bilangan ganjil

b.      Barisan bilangan ganjil adalah 1,3, 5, 7, 9, …

c.       Rumus mencari suku ke ke-n adalah Un = 2n – 1

Berikut adalah gambar pola dari bilangan ganjil

2.      Pola bilangan genap

Poal bilangan genap yaitu pola bilangan yang terbentuk dari bilangan – bilangan genap. Sedangkan pengertian dari bilangan genap sendiri memiliki arti suatu bilangan asli yang habis dibagi dua ataupun kelipatannya.

a.       Barisan bilangan genap adalah 2, 4, 6, 8, 10, ….

b.      Rumus untuk mencari suku ke-n adalah Un = 2n

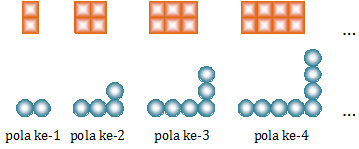
 Gambar pola bilangan genap adalah sebagai berikut

3.      Pola bilangan segitiga pascal

a.       Rumus mencari jumlah baris ke-n adalah 2n – 1

 Gambar pola bilangan segitiga pascal adalah sebagai berikut 

4.      Pola bilangan segitiga

a.       Barisan bilangan segitiga adalah 1, 3, 6, 10, 15, 21, …..

b.      Rumus mencari suku ke-n adalah Un = ½ n (n + 1 )

Gambar pola bilangan segitiga adalah sebagai berikut

5.      Pola bilangan persegi

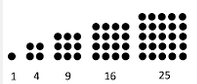
a.       Barisan bilangan persegi adalah 1, 4, 9, 16, 25, …..

b.      Rumus mencari suku ke-n adalah Un = n2

Gambar pola bilangan persegi adalah sebagai berikut

6.      Pola bilangan persegi panjang

a.       Barisan bilangan persegi panjang adalah 2, 6, 12, 20, 30, ……

b.      Rumus mencari suku ke-n adalah Un = n ( n + 1 )

Gambar pola bilangan persegi panjang adalah sebagai berikut 

7.      Pola bilangan Fibonacci

Pola bilangan fibanocci adalah pola bilangan dimana jumlah bilangan setelahnya merupakan hasil dari penjumlahan dari dua bilangan sebelumnya.

a.       Pola bilangan Fibonacci adalah 1, 1, 2, 3, 5, 8, 13, 21, 34, …..

b.      2 diperoleh dari hasil 1 + 1 3 diperoleh dari hasil 2 + 1, 5 diperoleh dari hasil 3 + 2 dan seterusnya

c.       Rumus mencari suku ke-n adalah Un = Un – 1 + Un – 2 

Gambar bilangan fibonic

8.      Pola bilangan pangkat tiga

Pola bilangan pangkat tiga adalah pola bilangan dimana bilangan setelahnya merupakan hasil dari pangkat tiga dari bilangan sebelumnya

Contoh pola bilangan pangkat tiga adalah 2, 8, 512, 134217728, …..

Keterangan : 8 diperoleh dari hasil 2 pangkat tiga, 512 diperoleh dari hasil 8 pangkat tiga, dan seterusnya

9.      Pola bilangan aritmatika

Pola bilangan aritmatika adalah pola bilangan dimana bilangan sebelum dan sesudahnya memiliki selisih yang sama.

Contoh pola bilangan aritmatika adalah 2, 5, 8, 11, 14, 17, ….

Suku pertama dalam bilangan aritmatika dapat disebut dengan awal ( a ) atau U1, sedangkan suku kedua adalah U2 dan seterusnya.

Selisih dalam barisan aritmatika disebut dengan beda dan dilambangkan dengan b.

Karena bilangan sebelum dan sesudahnya memiliki selisih yang sama, maka b = U2 - U1 = U3 – U2 = U4 – U3 = U5 – U4 = U6 – U5 = 3

Rumus mencari suku ke-n adalah Un = a + ( n – 1 ) b

Rumus mencari jumlah n suku pertama adalah Sn = n/2 ( a + Un ) atau 

Sn = n/2 (2 a + ( n – 1)b)

10.  Pola Bilangan Geometri

Pada pola bilangan geometri, suatu bilangan merupakan hasil perkalian bilangan sebelumnya dengan suatu bilangan yang tetap.

Rumus suku ke-n >> Un = ar^n-1 

Contoh:

1, 2, 4, 8, 16, 32, …

1, 3, 9, 27, 81, … 

 Latihan KLIK INI